When studying calculus, one of the first challenges students face is finding the derivative of a function that is written as a fraction, one function divided by another. The quotient rule is the formula that helps us do exactly that. It tells us how to find the rate of change for a ratio of two differentiable functions.
For example, if a function f(x)f(x)f(x) is divided by another function g(x)g(x)g(x), the quotient rule gives a clear method to find its derivative without breaking the logic of differentiation. It’s especially useful when both the numerator and denominator are complex and can’t be simplified easily.
A common mistake many learners make is assuming that the derivative of a fraction is just the fraction of the derivatives — meaning they wrongly think
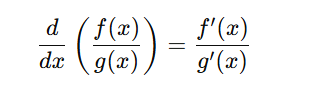
This looks neat but it’s completely wrong. Differentiation doesn’t work that way because both the numerator and denominator are changing with respect to xxx, and their changes are interdependent. The quotient rule accounts for this interaction correctly by applying both derivatives in a specific order.
In this guide, you’ll learn:
- The exact formula for the quotient rule.
- The proof and reasoning behind it.
- Step-by-step examples with clear solutions.
- The mistakes to avoid when applying it.
- And a set of practice problems to strengthen your understanding.
By the end, you’ll not only remember the formula — you’ll understand why it works and how to use it confidently in any calculus problem.
Basic Form of the Quotient Rule
The quotient rule is used to find the derivative of a function that’s formed by dividing one function by another.
If you have two differentiable functions f(x)f(x)f(x) and g(x)g(x)g(x), and g(x)≠0g(x) \neq 0g(x)=0, then the derivative of their quotient is given by:
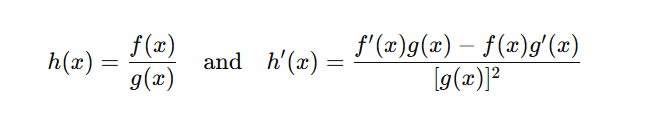
This formula might look complicated at first, but it follows a simple pattern that’s easy to remember.
Memory Trick: “Lo Dhi minus Hi Dlo, over Lo squared”
A popular way to remember the quotient rule is this short phrase:
“Low D High minus High D Low, over Low squared.”
Here’s what that means:
- Low (Lo) → the denominator g(x)
- High (Hi) → the numerator f(x)
- D High (Dhi) → the derivative of the numerator f′(x)
- D Low (Dlo) → the derivative of the denominator g′(x)
So, putting it all together:
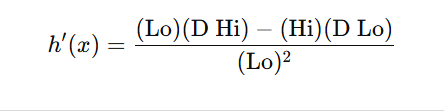
Breaking Down Each Part
Let’s interpret the components:
- Numerator f(x): the “top” function — the one being divided.
- Denominator g(x): the “bottom” function — the one doing the dividing.
- f′(x): tells you how fast the numerator is changing.
- g′(x): tells you how fast the denominator is changing.
- Square of the denominator [g(x)]2: ensures that the result is still properly scaled, keeping the overall structure of the fraction intact.
Simple Analogy for Data Analytics Students
Think of f(x) as profit and g(x) as cost. The quotient f(x) / g(x) then represents profit per unit cost, a ratio analysts often study.
When both profit and cost change with time, the quotient rule tells you how profit per cost is changing overall, accounting for both movements together, not separately.
This formula forms the foundation for understanding how ratios evolve, a concept that shows up everywhere in calculus, optimization, and data analytics.
Where the Quotient Rule Comes From (Intuitive Proof)
Many students memorize the quotient rule formula without knowing why it works, but understanding its origin makes it easier to remember and apply correctly.
Let’s build the rule from something you already know: the product rule.
Step 1: Rewrite the quotient as a product
We start with: h(x)=f(x)/g(x)
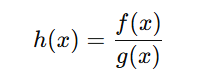
We can rewrite this as: h(x)=f(x)⋅1/g(x)=f(x)⋅[g(x)]−1
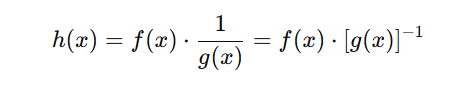
Now it looks like a product: one function f(x) multiplied by another function [g(x)]−1
Step 2: Apply the product rule
The product rule says: (uv)′=u′v+uv′(uv)’
Here, u=f(x)u and v=[g(x)]−1
So: h′(x)=f′(x)⋅[g(x)]−1+f(x)⋅d/dx[g(x)]−1
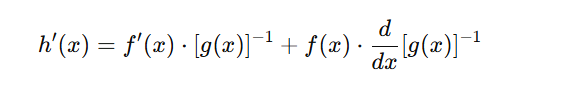
Step 3: Differentiate the reciprocal term
The derivative of [g(x)]−1 can be found using the chain rule:
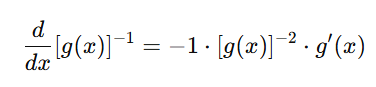
That simplifies to:
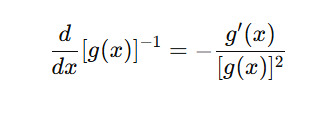
Step 4: Substitute back into the equation
Now plug that into our earlier expression for h′(x):
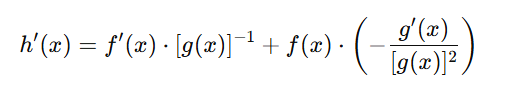
Simplify the terms:
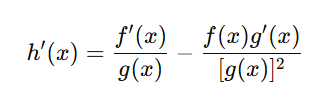
Step 5: Combine into a single fraction
To get a common denominator [g(x)]2
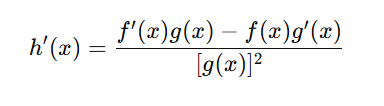
And that’s the quotient rule.
Why This Matters
Understanding this derivation helps you see that the quotient rule isn’t random, it’s just the product rule applied cleverly to a reciprocal function.
When you grasp this logic:
- You’re less likely to mix up the signs or the order in the numerator.
- You can reconstruct the formula even if you forget it.
- You understand how it ties into other differentiation rules.
Connection to Data Analytics
In data analytics, ratios like profit per customer or conversion rate are functions of changing quantities. The quotient rule shows how the rate of change of that ratio depends on both the numerator (e.g., profit) and denominator (e.g., customers).
By knowing why the formula works, analysts can better interpret whether changes in such metrics are driven more by the top or bottom variable, a key insight in performance optimization.
Step-by-Step Examples
Find the derivative of h(x)=x2/x+1
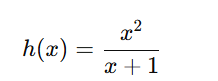
1) Identify fff and ggg
- f(x)=x2 (the numerator, “high”)
- g(x)=x+1 (the denominator, “low”)
2) Compute derivatives f′(x) and g′(x)
- f′(x)=2x
- g′(x)=1
3) Apply the quotient rule
Quotient rule:
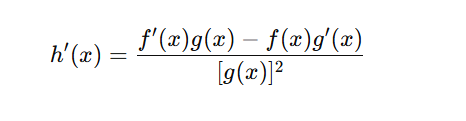
Substitute:
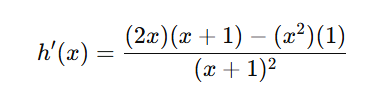
Simplify the numerator
Compute numerator step-by-step: (2x)(x+1)−x2= 2x2+2x−x2 = x2+2x
So h′(x)=x2+2x / (x+1)2
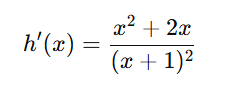
You can factor numerator if you like: h′(x)=x(x+2) / (x+1)2
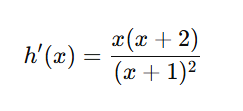
Quick tips shown by the examples
- Always identify f(x) (top) and g(x) (bottom) first.
- Compute f′(x) and g′(x) cleanly before substituting.
- Keep the numerator ordered as f′(x)g(x)−f(x)g′(x) order matters.
- If possible, simplify the original function first — that can make differentiation easier and reduce algebra.
- Use product rule on f(x)⋅[g(x)]−1 as a cross-check; it should give the same result.
Common Mistakes and Pitfalls When Using the Quotient Rule
1. Mixing up the order in the numerator
Mistake: Writing g′(x)f(x)−f′(x)g(x)
instead of f′(x)g(x)−f(x)g′(x)
Remember: “low d-high minus high d-low, over low squared.”
If you flip the order, your answer will have the wrong sign.
2. Forgetting to square the denominator
Students often stop at just g(x) in the denominator instead of [g(x)]2
Always finish with [g(x)]2
not just g(x).
3. Using the rule when simplification is easier
Before jumping into the quotient rule, check if you can simplify the fraction or rewrite as a product first.
Example:
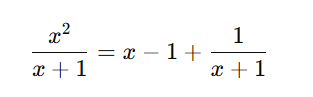
much easier to differentiate term by term.
4. Applying it where the denominator is zero
Remember: the derivative only exists where both f(x) and g(x) are differentiable and g(x)≠0
If g(x)=0 at a point, the function (and its derivative) are not defined there.
5. Losing track of parentheses
When substituting into the formula, missing parentheses can change the entire expression.
Always write:
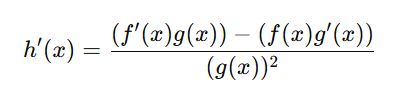
before simplifying.
Quick Recap:
✔ Keep order: f′g−fg′
✔ Square the denominator
✔ Simplify first if possible
✔ Check denominator ≠ 0
✔ Use parentheses carefully
When to Use the Quotient Rule vs Alternative Methods
The Quotient Rule is a powerful tool, but it’s not always the fastest or simplest way to find a derivative. Knowing when to use it (and when not to) will save time and help you avoid messy algebra.
When You Should Use the Quotient Rule
Use the quotient rule only when:
- The function is clearly a quotient of two differentiable functions i.e., it looks like h(x)=f(x)/g(x)
where both f(x) and g(x) are differentiable. - Simplifying the function before differentiating is not easy or possible.
Example: h(x)=x2+3x+1 / x3−2x
Both numerator and denominator are nontrivial functions, so the quotient rule is the cleanest choice.
When It’s Better to Simplify First
Sometimes, you can rewrite the expression using basic algebra or exponent rules before applying differentiation.
Example: h(x)=1 / x2 = x−2
Now you can simply use the power rule: h′(x)=−2x−3 =−2x−3
Much quicker no need for the quotient rule.
Another example: h(x)=x2 / x =x
Simplify before differentiating otherwise, you’d be doing unnecessary work.
Comparing to the Product Rule
Remember that: f(x) / g(x)=f(x)⋅[g(x)]−1
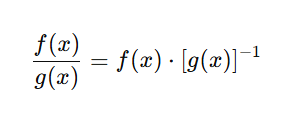
In some cases, applying the product rule to this rewritten form may feel more intuitive.
For instance: h(x)=sinx / x2 =sinx⋅x−2
Now apply the product rule: h′(x)=(cosx)(x−2)+(sinx)(−2x−3)
You’ll reach the same answer you’d get with the quotient rule but often with cleaner algebra.
Decision Flow for Choosing the Right Method
Here’s a quick way to decide:
| Situation | Best Method |
|---|---|
| Function is a clear fraction and cannot be simplified | Quotient Rule |
| Denominator is a single term (like x2, x3, etc.) | Simplify and use Power Rule |
| Function can be rewritten as a product | Product Rule |
| Denominator = 0 or not differentiable | Quotient Rule not valid |
Rule of Thumb
If simplification saves you time — take it.
If not — the quotient rule has your back.
Understanding when and why to choose each method will make your calculus problem-solving faster, cleaner, and less error-prone.
Applications and Real-World Context of the Quotient Rule
The quotient rule isn’t just a classroom exercise it shows up in many real-world situations where one changing quantity is divided by another. Whenever you have a ratio of two variables that both change, the quotient rule helps describe how fast that ratio changes.
1. Physics: Speed, Velocity, and Efficiency
In physics, you often deal with ratios like y=distance / time.
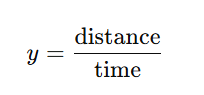
If both distance and time depend on another variable (say x or t), you need the quotient rule to find how the rate changes.
For example, if distance = f(x) and time = g(x):
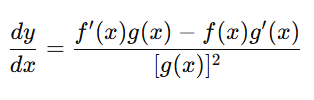
This tells us how speed or velocity changes when both the distance covered and the time taken vary at different rates, a key part of motion analysis.
2. Economics and Business Analytics
In economics, ratios like:
- Profit per unit = Profit ÷ Units Sold
- Cost efficiency = Output ÷ Input
- Return on investment (ROI) = Profit ÷ Investment
depend on quantities that both change with time or production levels.
The quotient rule lets analysts calculate marginal changes, for example, how ROI changes as investment and profit both vary.
This insight helps businesses decide how small changes in costs or investments will affect their overall efficiency.
3. Engineering and System Performance
Engineers often analyze performance metrics that involve ratios:
- Voltage per current
- Force per area (pressure)
- Efficiency = Output ÷ Input
If both the numerator and denominator depend on other parameters (temperature, load, resistance, etc.), the quotient rule provides the derivative, showing how sensitive the system’s performance is to these changes.
4. Data Analytics and Machine Learning
In data analytics, you frequently measure rates, like:
- Conversion rate = Clicks ÷ Impressions
- Engagement ratio = Active users ÷ Total users
When both parts change over time (e.g., both clicks and impressions fluctuate daily), the quotient rule helps analysts understand whether the rate change is driven more by the numerator or denominator, crucial for optimization and forecasting.
5. Everyday Example: Average Speed
Suppose you’re driving and want to know how your average speed is changing over time.
As both distance and time increase, the quotient rule helps compute how quickly your average speed is rising or falling — an essential insight for navigation systems and speed monitoring apps.
Takeaway
The quotient rule is more than a differentiation trick, it’s a model of how ratios evolve in real life.
Whether you’re studying physics, economics, or data analytics, understanding how one changing variable interacts with another gives you deeper insight into how systems behave.
Conclusion: Mastering the Quotient Rule
The quotient rule is one of the most practical tools in calculus, it helps you understand how the rate of change behaves when one changing quantity is divided by another.
From physics and engineering to economics and data analytics, it forms the foundation for analyzing ratios that evolve over time.






